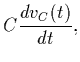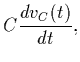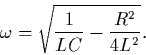Next: About this document ...
Linear RLC circuits are described by differential equations
of the second order.
From the KVL:
vs(t) = vR(t) + vC(t) + vL(t)
and KCL:
iR(t) = iC(t) = iL(t) .
Since
| vR(t) |
= |
R i(t) |
|
| vL(t) |
= |
 |
|
| iC(t) |
= |
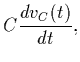 |
|
the second order differential equation in terms of vC(t) is:
Natural frequencies (also called time constants) of this
RLC circuit can be found by solving the
quadratic equation:
LC s2 + RC s + 1 = 0 .
They are of the form:
where
and
Note that for a circuit with positive R, L, and C, the real part of the
natural frequencies will always be negative.
The response of the circuit depends one the relative values of R, L, and C.
We distinguish cases:
-
Over-damped circuit: s 1 and s 2 real and distinct
-
Under-damped circuit: s 1 and s 2 complex conjugate numbers, and
-
Critically damped circuit:
s 1 = s 2 .



Next: About this document ...
Ljiljana Trajkovic
1998-11-14